In the previous section, we have learned about Decimal & Binary number systems. Generally in digital systems representation and operations on long strings is very common .We cannot effectively represent a number with more number of binary digits(long string) in binary number system. So to represent the long strings easily , we use another number system called “Hexadecimal number system”. Hexa decimal number system is widely used in assembly language coding.
Outline
ToggleHexa Decimal Number System
In the term Hexa decimal number system , the word ‘Hexa’ means 16. So as the name suggests, the Hexa decimal number system will have 16 values for representation of numeric that is – numbers from 0 to 9 and letters from A to F.
HEXA DECIMAL NUMBERS
The Hexa decimal numbers are shown in the below table. Here the 16 values represents that the numbers from 0 to 15. The numbers 0 to 9 are represented as usual but numbers from 10 to 15 are represented using alphabets A to F. The 16 numbers were used in different combinations to represent binary and decimal numbers.
After F, again the numbers starts from (10)16 , which is equal to 16 in decimal i.e (1× (16) )+ (0 ×(16))
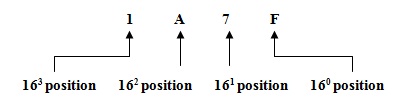
Note that each Hexa decimal number represents a group of four digits, called “Nibble”. In Hexa decimal number system , the position of digit is weighted as the powers of 16. This means that in a column, the value of a digit is sixteen times that of the digit to its right.
Ex: (10)16, (56)16, (3Fb1)16, (A51D0)16
Let’s see some more examples to understand this clearly
This Hexa decimal system is used in computer registers to store the addresses of the data. If we have to give a large number of binary strings, for suppose 1011110110001011111010110001101, it is very much difficult and create a lot of confusion. So computer uses Hexa decimal numbers in representation of such strings.
Conversion of Hexa Decimal Numbers
As we convert the binary number into decimal numbers and decimal numbers into binary numbers, we can also convert the Hexa decimal numbers into binary and decimal number systems.
Conversion from Binary to Hexa Decimal
To convert the binary numbers into Hexa decimal numbers, we group the binary digits as a set of four. If necessary, add zeros to complete the set. Next, write the corresponding number to the each group of the four digits.
Ex 1: Convert (0110101110001100)2 to Hexa decimal.
Given 0110101110001100, group the binary digits as a set of four digits.
0110 1011 1000 1100
6 B 8 C
So (0110101110001100)2 = (6B8C)16
Conversion from Hexa decimal to binary
To convert the Hexa decimal number into binary number, we follow the reverse steps explained above. First we write each digit of Hexa decimal number in binary form and then grouping the binary digits.
See some examples given below and then you will get a clear idea on this
Ex 1: convert 5A9 into binary
5 A 9
0101 1010 1001
So (5A9)16 = (10110101001)2
Conversion from Hexa decimal to decimal
To convert a Hexa decimal number to decimal number, we should write each digit / letter in the form of decimal number with base 10 and then the Hexa decimal ha to be written as the sum of powers of 16.
See the explained example,
Ex 1: Convert Hexa decimal number 1A9B into decimal.
1 A 9 B = 1 x 163 + A x 162 + 9 x 161 + B x 160 (writing powers of 16)
= 4096 + A (256) + 9 (16) + B (1)
= 4096 + 10 (256) + 144 + 11
= 6811
Therefore, (1A9B)16 = (6811)10
Conversion from decimal to Hexa decimal
The simple way to make a conversion from decimal to Hexa decimal number system is same as the conversion of decimal numbers to binary. There the repeated division process is done by 2 but as the Hexa decimal number is the base of 16, we should do the repeated division process by 16 instead of 2. The reminders are noted in the sequence of last to first.
Let’s learn this with an example: even number
746 ÷ 16 Quotient 10, remainder 46 Result > A
46 ÷ 16 Quotient 14, remainder 2 Result > E A
2 ÷ 16 Quotient 0, remainder 2 Result > 2 E A
So (746)10 = (2EA)16
Another example: odd number
3509 ÷ 16 Quotient 219, remainder 5 Result > 5
219 ÷ 16 Quotient 13, remainder 11 Result > B 5
13÷ 16 Quotient 0, remainder 13 Result > D B 5
So (3509)10 = (DB5)16
HexaDemical Numbers Representation
we have learned how to convert Hexa decimal numbers into other number systems and other number systems into Hexa decimal. Now let’s discuss about counting of Hexa decimal numbers.
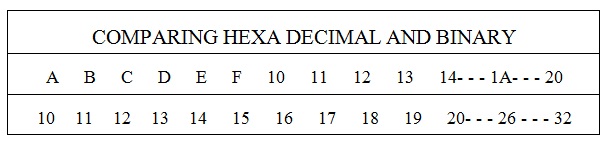
If we have to count the Hexa decimal numbers more than F, we will re-begin the count from binary digits. This is shown below.
Note:
Important and mandatory thing to remember in Hexa decimal number system , if we write (10)16 here, this means not 10. This is 1×(16) + 0×(16) in Hexa decimal. Similarly if we write 19 or 32 in Hexa decimal, they are not like Nineteen or Thirty two.they are 1× (16) + 9×(16 )and 3×(16 )+ 2×(16 )in Hexa decimal system. Simply,
(10)10 is not equal to (10)16
(19)10 is not equal to (19)16
(32)10 is not equal to (32)16
The highest positive decimal in decimal number system is 255; in this Hexa decimal system the highest number formed using the Hexa decimal digits is FF.This is equal to 255 in decimal number system and 1111 1111 in binary number system.
The least 3 bit Hexa decimal number is 10016 (25610) & highest is FFF16 (409510). The maximum 4 digit Hexa decimal number is FFFF16 (65,53510).
Representation of a HexaDecimal Number
If there are 4, 8, 12 or 16 binary digits, then it is easy to convert both decimal and binary numbers into Hexa decimal number by adding additional Hexa decimal numbers
For example, 10 1101 1000 1011 2 is a 14 digit binary number, and it is very large represent with 3 digit Hexa decimal number and too small to represent with 4 digit Hexa decimal number. So to make the representation comfortable, we will add 0’s to the left of most significant bit (MSB).
Then the main feature of the Hexadecimal Numbering System is that there are 16 counting digits from 0 to F and each digit having a weight (value) of 16 starting from the least significant bit (LSB). In order to distinguish Hexadecimal numbers from other numbers, a prefix is used. It is either a “#”, (Hash) or a “$” (Dollar sign before the actual Hexadecimal Number value
Ex: #A5CE or $A5CE.
Adding of Additional 0’s to a Binary Number
The main advantage of Hexa decimal number is that they are very compact to represent the addresses of fields or data, in computers. The Hexa decimal number will have fewer digits compared to binary digits. It is shown below.
Binary Number 0011 1110 0010 1011
Hexa decimal number 3 E 2 B
To make the representation comfortable, we will add 0’s to the left of most significant bit.
HexaDecimal Numbers Summary
- The word “Hexa” means 16. As the name implies, Hexa decimal number system will use a set of 16 digits. They are 0 – 9 & A – F.
- The Hexa decimal numbers are mostly used in computers to store addresses of data.
- These numbers are represented by using a ‘$’ (Dollar) sign or ‘#’ (Hash) sign before them. Ex: #A32C, $A32C.
- The least 3 bit Hexa decimal number is 10016 (25610) & highest is FFF16 (409510). The maximum 4 digit Hexa decimal number is FFFF16 (65,53510).
- In further chapters we will learn about octal number system and error decoding in different types of number systems.