Boolean Algebra Laws and Theorems

Boolean Algebra is a form of mathematical algebra that is used in digital logic in digital electronics. Albebra consists of symbolic representation of a statement (generally mathematical statements). Similarly, there are expressions, equations and functions in Boolean algebra as well.

The main aim of any logic design is to simplify the logic as much as possible so that the final implementation will become easy. In order to simplify the logic, the Boolean equations and expressions representing that logic must be simplified.

So, to simplify the Boolean equations and expression, there are some laws and theorems proposed. Using these laws and theorems, it becomes very easy to simplify or reduce the logical complexities of any Boolean expression or function.

The article demonstrates some of the most commonly used laws and theorem is Boolean algebra.

Basic Boolean Algebra Laws and Proofs

The basic rules and laws of Boolean algebraic system are known as “Laws of Boolean algebra”. Some of the basic laws (rules) of the Boolean algebra are

i. Associative law

ii. Distributive law

iii. Commutative law

iv. Absorption law

v. Consensus law

Associative Law

Associate Law of Addition

Statement:

Associative law of addition states that OR ing more than two variables i.e. mathematical addition operation performed on variables will return the same value irrespective of the grouping of variables in an equation.
It involves in swapping of variables in groups.

The Associative law using OR operator can be written as

A+(B+C) = (A+B)+C

Proof:

If A, B and C are three variables, then the grouping of 3 variables with 2 variables in each set will be of 3 types, such as (A + B), (B + C) and(C + A).

According to associative law

(A + B + C) = (A + B) +C = A + (B + C) = B + (C + A)

We know that, A + AB = A (according to Absorption law)

Now let’s assume that, x = A + (B + C) and y = (A + B) + C

According to associative law, we need to prove that x = y.

Now, find Ax = A [ A + (B + C) ]

= AA +A (B + C)

= A + AB + AC → since AA = A

= (A+ AB) + AC

= A + AC → since A + AB = A

= A → since A + AC = A

Therefore Ax = A

Similarly, for Bx = B [ A + (B + C) ]

= AB +B (B + C)

= AB + BB + BC

= AB + B + BC → since BB = B

= (B+ BC) + AB

= B + AB → since B + BC = B

= B → since B + AB = B

Using these above equations, we can say that the relation between A, B, C and + operator doesn’t change when multiplied by other variable like x, such as xy = yx = x = y.

yx = ((A + B) + C) x

= (A + B) x + Cx

= (Ax + Bx) + Cx

= (A + B) + C

= y xy = (A + (B + C)) y

= Ay + (B + C) y

= Ay + (By + Cy)

= A + (B + C)

= x

So x = y, which means A + (B + C) = (A + B) + C = B + (A +C)

Example

Take three variables 0, 1 and 0, then

According to associative law,

(0 + 1) + 0 = 0 + (1 + 0)

1 + 0 = 0 + 1

1 = 1

Hence associative law is verified.

Hence the Associative law is proved, (A + B + C) = (A + B) +C = A + (B + C) = B + (C + A)

Associate Law of  Multiplication

Statement:

Associative law of multiplication states that ANDing more than two variables i.e. mathematical multiplication operation performed on variables will return the same value irrespective of the grouping of variables in an equation.

The Associative law using AND operator can be written as

A * (B * C) = (A * B) * C

Distributive law

This is the most used and most important law in Boolean algebra, which involves in 2 operators: AND, OR.

Statement1:

The multiplication of two variables and adding the result with a variable will result in same value as multiplication of addition of the variable with individual variables.

In other words, ANDing two variables and ORing the result with another variable is equal to AND of ORing of the variable with the two individual variables.

Distributive law can be written as

A + BC = (A + B)(A + C)

This is called OR distributes over AND.

Proof:

If A, B and C are three variables then

A + BC = A * 1 + BC → since A*1 = A

= A (1 + B)+ BC → since 1 + B = 1

= A * 1 + AB + BC

= A *(1 + C) + AB + BC → since A*A = A*1 = A

= A *(A + C) + B (A + C)

= (A + C) (A + B)

A + BC = (A + B) (A + C)

Hence, distributive law is proved.

Statement 2:

The addition of two variables and multiplying the result with a variable will result in same value as addition of multiplication of the variable with individual variables.

In other words, ORing two variables and ANDing the result with another variable is equal to OR of ANDing of the variable with the two individual variables.

Distributive law can be written as

A (B+C) = (A B) + (A C)

This is called AND distributes over OR.

Proof:

A (B + C) = A (B*1) + A (C*1) → since 1 * B = B, 1 * C = C

= [(AB)*(A*1)] + [(AC) *(A*1)]

=[(AB) * A] + [(AC) *A]

= (A +1) (AB + AC)

= (AB +AC) → since 1 + A = 1

Hence, distributive law is proved.

Example:

Take three variables 0, 1 and 0, then

According to distributive law,

0 (1 + 0) = (0*1) + (0*0)

0 (1) = (0) + (0)

0 = 0

Hence,distributive law is verified.

Commutative law

Statement:

Commutative law states that the inter-changing of the order of operands in a Boolean equation does not change its result.

• Using OR operator → A + B = B + A
• Using AND operator → A * B = B * A

This law is also has more priority in Boolean algebra.

Example:

Take 2 variables 1 and 0, then

1 + 0 = 0 + 1

1 = 1

Similarly,

1 * 0 = 0 * 1

0 = 0

Absorption Law

Absorption law involves in linking of a pair of binary operations.

i. A+AB = A

ii. A(A+B) = A

iii. A+ĀB = A+B

iv. A.(Ā+B) = AB

3rd and 4th laws are also called as Redundancy laws.

Statement 1: A + AB = A

Proof:

A + AB = A.1 + AB → since A.1 = A

=A(1+B) → since 1 + B = 1

= A.1

= A

Statement 2:A (A + B) = A

Proof:

A (A + B) = A.A + A.B

= A+AB → since A . A = A

= A (1 + B)

= A.1

= A

Statement 3:A + ĀB = A + B

Proof:

A + ĀB = (A + Ā) (A + B) → since A+BC = (A+B)(A+C) using distributive law

= 1 * (A + B) → since A + Ā = 1

=A + B

Statement 4: A * (Ā+B) = AB

Proof: A * (Ā + B) = A. Ā + AB

= AB → since A Ā = 0

Duality Principle in Boolean algebra

Statement:

Duality principle states that “The Dual of the expression can be achieved by replacing the AND operator with ORoperator, along with replacing the binary variables, such as replacing 1 with 0 and replacing 0 with 1”.
This law explains that, replacing the variables doesn’t change the value of the Boolean function.

But while interchanging the names of the variables, we must change the binary operators also. “If the operators and variables of an equation or function that produce no change in the output of the equation, though they are interchanged is called “Duals”.

The Duality principle is also known as “De Morgan Duality”, which states that ‘Interchanging of Duals pairs in Boolean algebra will result in same output of the equation’.

There is one special type of operation in duality that is ‘Self-dual’.A self-dual operation processes the input to the output, without making any changes to it. So this is also called “Do nothing operation”.

Example:

If we have the Boolean equation like A + B = 0, then the equation formedby replacing the variable 0 with 1 and replacing the OR operator with AND operator is A * B = 1. This means both the Boolean functions are represents the operation of logic circuit.

As per Duality principle, if A, B are two variables then both the equations A + B = 0 and A * B = 1 are true in case of same logic circuit.

Simplification of Boolean functions using Duality

Example of simplification of Boolean function by using Duality concept

(A +B’ C)’ = A’ B C + A’ B C’ + A’ B’ C’

= A’ B (C + C’) + (B + B’) A’ C’

= A’ B + A’ C’ – – – – – – – -> (1)

Taking inverse on both sides, the equations becomes

(A +B’ C) = (A + B’) (A + C) – – – – – – – -> (2)

If we observe the equations 1 and 2, we can observe that the AND operator and OR operators are interchanged. Hence Duality theorem is proved.

Boolean functions can be simplified by using max terms (SOP) and mean terms (POS) method, based on Duality principle.

SOP method means, sum of products. In this method, the max terms of Boolean variables are written as their sum of products.

POS method means, product of sums. In this method, the min terms of Boolean variables are written as their product of sums.

We will discuss these topics briefly, in our further tutorials.

De Morgan’s Theorem

Boolean algebra involves in binary addition, binary subtraction, binary division and binary multiplication of binary numbers. Similar to these basic laws, there is another important theorem in which the Boolean algebraic system mostly depends on. That is De Morgan’s law.

This can be also known as De Morgan’s theorem. This law works depending of the concept of Duality. Duality means interchanging the operators and variables in a function, such as replacing 0 with 1 and 1 with 0,AND operator with OR operator and OR operator with AND operator.

De Morgan’s law is like extension of the Duality principle. De Morgan proposed 2 theorems, which will help us in solving the algebraic problems in digital electronics.

The De Morgan’s statements are,

Statement 1:

“The negation of conjunction is the disjunction of the negations”. Or we can define that as “The compliment of the product of 2 variables is equal to the sum of the compliments of individual variables”.

(A.B)’ = A’ + B’

Statement 2:

“The negation of disjunction is the conjunction of the negations”. Or we can define that as “The compliment of the sum of two variables is equal to the product of the compliment of each variable”.

(A + B)’ = A’.B’

Truth Tables

The De Morgan’s laws are simply explained by using the truth tables.

The truth table for De Morgan’s first statement((A.B)’ = A’ + B’) is given below.

 

So the De Morgan’s first law can also be expressed as “not (A and B) is equal to (not A) or (not B)”.

The truth table for De Morgan’s second statement ((A + B)’ = A’.B’) is given below.

So the De Morgan’s first law can also be expressed as “not (A or B) is equal to(not A) and (not B)”.

DeMorgan’s Theorem in Gates

The De Morgan’s theorem can be proved by using basic logic gates such as AND gates and OR gates.

For statement 1: (A.B)’ = A’ + B’

The output of aNAND gate (AND gate with a NOT gate at its output side) is equal to output of the gate formed by connecting two NOT gates at the inputsof OR gate. This can be said as,

NANDgate= Bubbled OR gate

For statement 2: (A + B)’ = A’.B’

The output of a NOR gate (OR gate with a NOT gate at its output side) is equal to output of the gate formed by connecting two NOT gates at the inputs of AND gate. This can be said as,

NOR gate= Bubbled AND gate

Let’s see some examples to understand how the De Morgan’s theorem is used to simplify the Boolean equations.

Example 1:

Simplify the below Boolean equation by using De Morgan’s theorem.

F =(((A .B ̅ ) ̅).(B ̅ + C)) ̅

Sol:

Given F = (((A .B ̅ ) ̅).(B ̅ + C)) ̅

= (((A .B ̅ ) ̅)) ̅ + ((B ̅ + C)) ̅

= (A .B ̅) + (B ̅ ̅ .C ̅)

= (A .B ̅) + (B.C ̅)

Therefore the simplified form of the given equation is F = (A .B ̅) + (B.C ̅)

Example 2

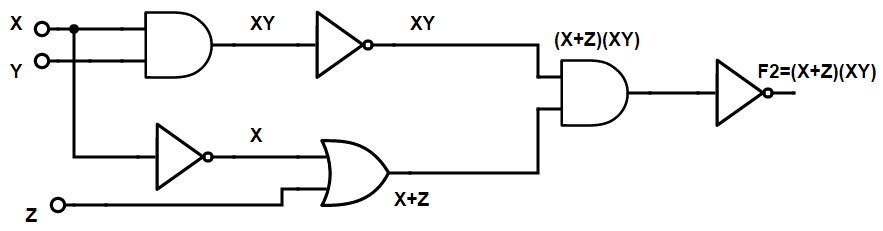
Simplify the poorly designed logic circuitand find the simplified Boolean equation for the output equation.

Sol:

In the given circuit, the output equation is,

F2= ((A ̅ + C).((AB) ̅)) ̅

=((A ̅ + C) ̅) + (AB) ̅ ̅

= ((A ̅ + C) ̅) + AB

= (A ̅ ̅C ̅) + AB

= (AC ̅)+ (AB)

Therefore the simplified output of the given circuit isF2 = (AC ̅) + (AB).

Consensus Theorem

Consensus theorem is an important theorem in Boolean algebra, to solve and simplify the Boolean functions.

Statement

The consensus theorem states that the consensus term of a disjunction is defined when the terms in function are reciprocals to each other (such as A and A ̅). Consensus theorem is defined in two statements (normal form and its dual). They are

AB + ĀC+BC = AB+ĀC

(A+B)( Ā+C)(B+C) = (A+B)( Ā+C)

Proof of Consenus theorem

Statement 1: AB + ĀC+BC = AB+ĀC

AB+ĀC+BC = AB + ĀC + BC.1

= AB + ĀC + BC (A + Ā) → since A + Ā = 1

= AB + ĀC + ABC + ĀBC

= AB (1 + C) + ĀC (1 + B)

= AB + ĀC → since 1 + B = 1 + C = 1

Example

By using consensus theorem, prove that A’BD’ + BCD + ABC’ + AB’D = BC’D’ + AD + A’BC

Sol:

A’BD’ + BCD + ABC’ + AB’D = A’BD’ + BCD + ABC’ + AB’D + A’BC + BC’D’ + ABD

= AD + A’BD’ + BCD + ABC’ + A’BC + BC’D’

= AD + A’BC + BC’D’

Dual of Consensus Theorem

The statement of dual of consensus theorem is

(A+B)(B+C)(A’+C) = (A+B)(A’+C)

Proof

Step 1: Reducing the left side of the equation

(A + B) (B + C) (A’ + C) = ((A + B) (B + C)) (A’ + C)

=(AB + AC + BB + BC)(A’+C)

= (AB + AC + B + BC) (A’ + C)

=(AB + AC + (B + BC)) (A’ + C)

= (AB + AC + B) (A’ + C)

= (B + AB + AC) (A’ + C)

= ((B + AB) + AC) (A’ + C)

= (B + AC) (A’ + C)

= A’B + BC + AA’C + ACC

= A’B + BC + 0 + AC

= A’B + BC + AC

Step 2: Reducing the right side of the equation

(A+B) (A’+C) = AA’ + A’B + AC + BC

=0 + A’B + AC + BC

=A’B + AC + BC

Now we can see that, R.H.S. = L.H.S.

Hence,the Dual of the consensus theorem is proved.

Shannon’s Expansion Theorems

The well known theorist and mathematician, Claude Shannon proposed some formulae after researching in the simplification of Boolean algebraic functions. These are known as Shannon’s Expansion Theorem. These are used to expand a Boolean function about a single variable.

Theorem 1:

f (A1,A2, A3, . . . . Ai, . . . . An) = Ai . f (A1, A2, A3, . . . . 1, . . . An)+ A ̅i . (A1, A2, A3, . . . . 0, . . . An)

Example:

f (A, B, C, D, E, F) = C . f(A, B, 1, D, E, F) + C ̅. f (A, B, 0, D, E, F)

Theorem 2:

f (A1¬, A2, A3, . . . . Ai, . . . . An) = [Ai + f (A1, A2, A3, . . . . . . An)]. [A ̅i + (A1, A2, A3, . . . . 1, . . . An)]

Example:

f (A, B, C, D, E, F) = [C + f (A, B, 0 , D, E, F)] .[C ̅+ f (A, B, 1, D, E, F)]

Simplification of Boolean functions using Shannon’s Expansion Theorems

Practice 1:

Expand the given Boolean function using Shannon’s expansion theorem.

f (A, B, C, D) = A B ̅ + (A C + B) D

Sol: Given function is

f (A, B, C, D) =A B ̅ + (A C + B) D

= A [1. B ̅ + (1 . C + B) D] + A ̅ [0 . B ̅ + (0 . C + B) D]

= A [B ̅ + (C + B) D] +A ̅ [B D]

= A B ̅ + A (C + B) D + A ̅B D

Practice 2:

Expand the given Boolean function using Shannon’s expansion theorem.

f (A, B, C, D) = A ̅C+ (B + AD) C

Sol:

Given function is

f (A, B, C, D) = A ̅ C+ (B + AD) C

= A [1 ̅ . C + (B + 1 . D) C] + A [0 ̅ . C + (B + 0 . D) C]

= A [0 . C + (B + D) C] + A [1 . C + (B + 0 . D) C]

= A (B +D) C + A ̅(C + BC)

Shannon’s Reduction Theorems

Shannon’s reduction Theorems are used to reduce a Boolean function about a single variable.

Theorem 1:

Ai. f(A1, A2, A3, . . . . Ai, . . . . , An) = Ai . f(A1, A2, A3, . . . . 1, . . . . , An)

Ai+ f(A1, A2, A3, . . . . Ai, . . . . , An) = Ai+ f(A1, A2, A3, . . . . 0, . . . . , An)

Example:

B . f (A, B, C, D, E, F) = B . f (A, 1, C, D, E, F)

B + f (A, B, C, D, E, F) = B + f (A, 0, C, D, E, F)

Theorem 2:

(A_i ) ̅ . f(A1, A2, A3, . . . . Ai, . . . . , An) = (A_i ) ̅. f(A1, A2, A3, . . . . 0, . . . . , An)

(A_i ) ̅+ f(A1, A2, A3, . . . . Ai, . . . . , An) = (A_i ) ̅ + f(A1, A2, A3, . . . . 1, . . . . , An)

Example:

B ̅ . f (A, B, C, D, E, F) = B ̅. f (A, 0, C, D, E, F)

B ̅+ f (A, B, C, D, E, F) = B ̅+ f (A, 1, C, D, E, F)

Simplification of Boolean functions using Shannon’s Reduction Theorems

Practice 1:

Expand the given Boolean function using Shannon’s reduction theorem.

f (A, B, C, D) = A [A ̅ (B + C) + (A + D)]

Sol: Given function is

f (A, B, C, D) = A [A ̅ (B + C) + (A + D)]

= A . [ 1’ (B +C) + (1 + D)]

= A . [0 (B +C) + (1 + D)

= AD

Practice 2:

Expand the given Boolean function using Shannon’s reduction theorem.

f (A, B, C, D) = A + A’ B + A C’ (B + C) (B + D)

Sol: Given function is

f (A, B, C, D) = A + A’ B + A C’ (B + C) (B + D)

= A + 0’ B + 0 C’ (B +C) (B + D)

= A + 1 . B

= A + B